Abstract
The quasi-2-day wave (Q2DW) is a large temperature disturbance in the austral summer-time mesosphere. Its decay-phase movement and phase-speed are poorly understood. Q2DW events observed by the microwave limb sounder (MLS) onboard the NASA Aura satellite reveal that during the temperature Q2DW’s decay-phase, the Q2DW temperature disturbance is still substantial, but its phase-speed reduces exponentially, on average, from around −70 to −20 m/s in around 30-days. Observations also reveal significant interannual variability in these phase-speed values. Q2DW events simulated by the extended Canadian middle atmosphere model (eCMAM) reveal that during the Q2DW decay-phase, the temperature Q2DW phase-speed is strongly correlated with the summer mesosphere easterly jet (SMEJ) wind values. eCMAM also shows that the phase-speed interannual variabilities partially reflect the interannual variabilities of the SMEJ. Planetary-wave diagnostics indicate that during the Q2DW’s decay phase, there is still an active transfer of momentum from the SMEJ into Q2DW. The model simulations therefore indicate that the SMEJ plays a substantial role in the decaying temperature Q2DW phase-speed variabilities observed by MLS. This adds to our knowledge of how the SMEJ affects the Q2DW.
Similar content being viewed by others
Introduction
Over the winter troposphere and stratosphere, the winter polar vortex either directly or indirectly affects weather systems like fronts or storms as well as space weather conditions1,2,3,4,5. The vortex can affect these tropospheric weather systems and space weather indirectly through planetary-scale waves6,7. Space weather refers to the conditions of our ionosphere/thermosphere region (between ~ 90 km and 1000 km) and they are important to spacecraft, and other space-based technologies8. Planetary-scale waves are oscillating perturbations that encompasses an entire latitude circle. These waves can form when the vortex wiggles north and/or south of their initial latitude band.
Over the Austral summer hemisphere, the summer mesosphere easterly jet (SMEJ) isn’t known to affect tropospheric weather systems, but it is known to affect space weather indirectly through its generation of and impacts on the largest planetary-scale wave in the region, the quasi-2-day wave (Q2DW)9,10,11,12,13,14. The Q2DW manifests in a time-series of temperature, winds and tracer longitudinal profiles as a westward propagating wave-like feature whose period varies between 40 and 60 h and whose wavenumber is 3. Eventually, the wave becomes a normal mode. As a normal mode, SMEJ variability continues to affect Q2DW amplitudes and phases15,16,17,18,19,20,21. Also, as a normal mode, the Q2DW affects space weather through changes in ionospheric electron density and thermospheric composition14,17.
This study adds to our knowledge of how the SMEJ affects the Q2DW component of temperature (hereafter referred to as Q2DW unless otherwise specified). In this study, we focus on the Q2DW phase-speed variabilities on days after its highest amplitude. We call this its decay phase (more on this definition later). This study analyzed multiple decades of Q2DW events over the Austral summer hemisphere (hereafter just “summer hemisphere” unless otherwise stated) simulated by the extended Canadian Middle Atmosphere Model (eCMAM) and observed by the Microwave Limb Sounder (MLS) instrument onboard the NASA Aura satellite. This study finds that during the Q2DW decay phase (the term decay phase in this work only refers to Q2DW’s decay phase), the SMEJ has substantial control of the Q2DW phase-speed’s variabilities. This suggests that the SMEJ has substantial control of the zonal movement of decaying Q2DW temperature perturbations. This dynamic is found to be consistent across multiple decades of simulated Q2DW events which may explain the similarities in the interannual variability of decaying-Q2DW phase-speed and SMEJ wind values. Unlike the winter polar vortex, the SMEJ isn’t known to frequently drive the movement of temperature structures. Often, this is because most temperature variability in the region is either driven by diabatic and/or adiabatic processes22. When temperature structures do seem to move, they often most likely belong to a moving atmospheric wave. This work presents another rare case of the SMEJ substantially driving the movement of an independent temperature structure. This is like the substantial control of the winter polar vortex and/or the subtropical jet on the horizontal movement of tropospheric weather disturbances like fronts or storms. These results add to our knowledge of how background winds affect the Q2DW by focusing on the Q2DW phase-speed during the Q2DW’s decay phase. Most of the previous efforts focused on the Q2DW amplitudes and phases during the Q2DW’s generation and saturation phases9,10,11,12,13,16,17.
MLS-observed Q2DW phase-speed variability
The phase-speed of temperature’s Q2DW component is the focus of this work. Apart from being a wave characteristic, this work notes that over a latitude circle, it is possible for the calculated phase-speed to match the wind-speed of a nearby jet also flowing in the same circle. This can happen if temperature spatial structures barely change for an extended period. This allows the jet to move it in a way that makes the structures act like a wave. Figure 1a shows a snap-shot of temperature fields at ~ 82 km during a Q2DW event as simulated by the extended Canadian Middle Atmosphere Model (eCMAM). Visually inspecting a time-series of these polar maps shows that the wave has a period of roughly ~ 1.5 days. Over the specific latitude 45S, this would give a phase-speed of around −70 m/s (negative is for westward motion and positive is for eastward motion). A more convenient approach is to use two-dimensional least-squares fit (see "Methods") to identify the dominant wave and calculate its phase-speed. In this example, two-dimensional least-squares fit analysis yields a time-series spectra shown in (Fig. 1b), and it shows that the dominant period is indeed ~ 1.5 days translating to a phase-speed of around −70 m/s. This work applied two-dimensional least-squares fit on eCMAM simulations and temperature observations from the microwave limb sounder (MLS) onboard the NASA Aura satellite (see "Methods").
(a) Snap-shots of eCMAM southern hemispheric temperature at 82 km on 00UT, day 23 in year 2002. (b) Amplitude spectra of quasi-2-day wave with wavenumber 3 at latitude 40S and altitude 82 km. (c) 18-year average of MLS observed Q2DW amplitude zonal profile on the 30th day after peak-Q2DW-day. (d) 18-year average of MLS observed Q2DW amplitude and phase-speed from 2005 till 2023 at latitude 40S and altitude 82 km. Both time-series spans from the 5th day till the 60th day of each year.
Unlike previous Q2DW studies, this work focuses solely on the decay-phase of a Q2DW. We define the decay-phase of the Q2DW as the 30 days after a Q2DW event reaches its highest amplitude in temperature fields. A feature tracking algorithm (see "Methods") is used to determine when a Q2DW event reaches its highest amplitude. This date is hereafter referred to as “peak-Q2DW-day”. Figure 1c shows the 18-year (from 2005 to 2023) average of MLS Q2DW amplitude on the 30th day after peak-Q2DW-day. It shows the peak amplitude is still at least 4 K and is located at around latitude 40S and altitude 82 km. This suggests that after 30 days of peak-Q2DW-day, there is still a significant Q2DW temperature disturbance. The time-series of Q2DW phase-speed (SMEJ wind values) between peak-Q2DW-day and the 30th day after peak-Q2DW-day is hereafter referred to as “decaying-Q2DW phase-speed” (“decay-phase-SMEJ wind values”). Figure 1d shows the average of all MLS Q2DW amplitude and phase-speed from 2005 to 2023 at latitude 40S and altitude 82 km. Both time-series span from the 5th day till the 60th day of each year. Figure 1d shows that on average, it takes around 30 days for the Q2DW amplitude to go from peak value to less than 2 K. Hence, we choose our decay-phase to last 30 days. Figure 1d also shows that on average, the Q2DW phase-speed gradually changes from around −70 to −20 m/s during this decay-phase. The errorbars indicate significant interannual variability. The rest of the manuscript shows that these short-term and interannual variability are connected to the SMEJ. Pendlebury23 hinted at this similarity in a few Q2DW events simulated by eCMAM. Here, we establish and further probe this using all Q2DW events simulated by eCMAM.
The change in Q2DW phase-speed from −70 to −20 m/s clearly indicates that the wave is no longer “quasi-2-day” in period. However, the wave’s phase-speed never stays at the same value long enough to be labeled according to its corresponding period. The wave’s phase-speed continues to change at an exponential rate. Hence, instead of labeling the Q2DW in terms of its new period, we just label the wave as “decaying Q2DW”. Retaining the term Q2DW signifies that the wave began as a Q2DW and not some randomly appearing wave with some phase-speed between −70 and −20 m/s.
High correlation between Q2DW phase-speed and summer mesosphere easterly jet
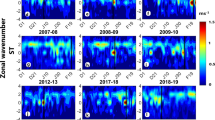
This work first reports that the decaying-Q2DW phase-speed and decay-phase-SMEJ wind values are highly correlated and very similar in magnitude around the area of the SMEJ. For each year, we calculated the correlation and root-mean-square (RMS) between decaying-Q2DW phase-speed and decay-phase-SMEJ wind values. Supplementary Figure S2 shows a sample correlation and RMS zonal profile for one Q2DW event. We also calculated the average of Q2DW amplitudes during the Q2DW decay-phase (hereafter referred to as decaying-Q2DW amplitudes). Figure 2a,b shows the average of all these correlation and RMS zonal-profiles from model year 1979 to 2010, respectively. We also took their standard deviation (Supplementary Figure S3). Figure 2c shows the average of decaying-Q2DW amplitude zonal-profiles. Figure 2a consistently shows a high positive correlation of at least 0.6 throughout the mid-latitude summer mesosphere which is also the location of the SMEJ. Figure 2b adds that these areas with high correlation also coincide with regions of low RMS (within ± 25 m/s). Figure 2c indicates that these regions also coincide with areas of peak Q2DW amplitudes. Standard deviation values confirm the consistency of high positive correlations and low RMS values throughout the mid-latitude mesosphere.
(a) 31-year average of the yearly correlation zonal-profile between decaying Q2DW phase-speed and decay-phase SMEJ wind values. (b) 31-year average of the yearly RMS zonal-profile between decaying Q2DW phase-speed and decay-phase SMEJ wind values. (c) 30-year average of decaying Q2DW amplitude. See the main text for more details.
This work next reports that Q2DW phase-speed values and SMEJ wind values have similar interannual variabilities. For each year’s Q2DW event, we averaged the Q2DW phase-speed during the Q2DW decay-phase. We refer to this as “decaying-Q2DW average phase-speed”. We did the same with the SMEJ wind values and we refer to this as “decay-phase-SMEJ average wind”. This provides a zonal profile of decaying-Q2DW average phase-speed and decay-phase-SMEJ average wind each year. Then, over each latitude-altitude bin, we took the correlation and RMS between the decaying-Q2DW average phase-speed and decay-phase-SMEJ average wind. Figure 3 shows these correlations and RMS profiles as well as sample time-series. Figure 3a,b shows high correlation and low RMS in their interannual variabilities over much of the mid-latitude southern mesosphere. Figure 3c shows sample time-series of decaying-Q2DW average phase-speed and decay-phase-SMEJ average wind over the boxed region. Figure 3d shows their scatter-plot. Figure 3c,d confirm the high correlation and low RMS between them.
(a) Correlation between decaying Q2DW phase-speed and SMEJ wind values averaged between the day of peak Q2DW amplitude and the 30th day after this peak. (b) RMS between the same parameters in (a). Contour-filled regions in (a) and (b) are areas of statistically significant correlation at 95% level. (c) Sample time-series located inside the box in (a) and (b). (d) Scatter plot of the two time-series in (c).
Interannual variability of decaying-Q2DW average phase-speed
Here, we explore the decaying-Q2DW average phase-speed’s interannual variabilities. The simulated decaying-Q2DW average phase-speed and decay-phase SMEJ average wind values can be reconstructed using the ENSO index, QBO index and F10.7 index. Figure 4a shows the correlation between decay-phase-SMEJ average wind values and its reconstruction using the ENSO index, QBO index and F10.7 index. Figure 4b shows the same as Fig. 4a but for decaying-Q2DW average phase-speed. Figure 4c,d show sample time-series of these two parameters over the boxed location. Figure 4a,b shows a statistically significant high correlation throughout the mid-latitude southern mesosphere but the correlation with the decay-phase SMEJ average wind values is higher. Supplementary Figure S4a–c show the individual correlations of the decay-phase-SMEJ average wind values with the indices. Supplementary Figure S5a–c show the individual correlations of the decaying-Q2DW average phase-speed with the indices. These results suggest that the interannual variability of decaying-Q2DW average phase-speed may partially reflect the combined influence of these interannual phenomena on the decay-phase SMEJ average wind values.
(a) Correlation between eCMAM decay-phase SMEJ average wind values and its reconstruction using ENSO index, QBO index and F10.7 index. (b) Correlation between eCMAM decaying-Q2DW average phase-speed and its reconstruction using ENSO index, QBO index and F10.7 index. (c) Sample SMEJ average wind values time-series and its reconstruction. (d) Sample decaying-Q2DW average phase-speed and its reconstruction. Both sample time-series in (c) and (d) are average of time-series found inside black boxes in (a) and (b), respectively. Contour-filled regions in (a) and (b) are areas of statistically significant correlation at 95% level.
The MLS-observed decaying Q2DW phase-speed interannual variabilities also has correlations with and can also be reconstructed using ENSO index, QBO index and F10.7 index. Figure 5a shows the same as (Fig. 4b) but for the MLS decaying Q2DW phase-speed. Note that the years that MLS covers are different from eCMAM. Figure 5a also shows statistically significant high correlation in the mid-latitude southern mesosphere but the areas are scattered unlike eCMAM simulations. Figure 5b shows a sample time-series over the boxed area in (Fig. 5a). Supplementary Figure S6 shows the same as Figure S5 but for MLS-observed phase-speed. We don’t have observations of SMEJ wind values to confirm whether these are partially reflective of the interannual variability of SMEJ wind values. Instead, we use the eCMAM simulations to suggest that these MLS Q2DW phase-speed interannual variability may be reflective of SMEJ wind values.
(a) Correlation between MLS decaying-Q2DW average phase-speed and its reconstruction using ENSO index, QBO index and F10.7 index. (b) Sample decaying-Q2DW average phase-speed and its reconstruction. Sample time-series in (b) is average of time-series found inside black boxes in (a). Contour-filled regions in (a) are areas of statistically significant correlation at 95% level.
Momentum transfer from the summer mesosphere easterly jet into the wave
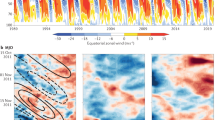
Planetary wave diagnostics on the model simulations confirm the presence of active wave-mean flow dynamics in the same area where there is a high correlation between decaying-Q2DW phase-speed and decay-phase SMEJ wind values. Figure 6 shows the 30-year average of these diagnostics on the 10th, 20th and 30th day after peak-Q2DW-day. Figure 6 provides causal mechanisms behind the highest correlations found in (Fig. 2). Figures 6a–c shows that even after 30 days, the average location of the peak in Q2DW amplitude is still distinguishable which suggests that the Q2DW hasn’t completely dissipated yet. Figures 6d–f show that the highest divergence values are above 65 km. The area of highest positive EP flux divergence is located between latitudes 40 and 20S and is vertically sandwiched between regions of negative EP flux divergence. The EP flux vectors are pointed away from areas of positive EP flux divergence and into areas of negative EP flux divergence. Figures 6g–i further indicate that below 80 km, the baroclinic instability may be a source for the positive EP flux divergence.
Left, middle and right column are 30-year averages of planetary-wave diagnostics on the 10th day, 20th day and 30th day after peak of Q2DW amplitude, respectively. (a–c) Zonal profiles of Q2DW amplitude and EP Flux vectors. Contour-filled regions are regions where EP Flux divergence is positive. (d–f) Zonal profiles of EP Flux vectors and EP Flux divergence. Contour-filled regions are regions where EP Flux divergence is positive. (g–i) Zonal profiles of daily-mean zonal-mean zonal winds, \({\overline{q} }_{\phi }\) and critical lines. Contour-filled regions of the background zonal wind are areas where \({\overline{q} }_{\phi }<0\) which is a crucial but insufficient condition for baroclinic/barotropic instability.
Figure 2a shows that above 65 km, the highest correlations of at least 0.8 are between latitude 40S and 20S and their altitude reaches up to around 85 km. Figure 2b further indicates that over the mid-latitudes, the regions of high correlation between 65 and 85 km have relatively low RMS. Figure 2a,b and Figs. 6d–f indicate that over these areas of high correlation and low RMS, we see the presence of two wave-mean flow dynamics occurring simultaneously: (1) the SMEJ is depositing its momentum into the Q2DW and (2) the Q2DW is depositing its momentum into the SMEJ. Knowing the current state of the decaying Q2DW’s amplitude and phase-speed, the areas of the first dynamic are areas where SMEJ conditions no longer amplify the Q2DW, but it can control the decaying Q2DW’s phase-speed via momentum transfer. On the other hand, the areas where the second wave-mean flow dynamic dominate are areas where the wave is simply decaying and hence its phase-speed to gradually approaching 0. Taken together, these planetary wave diagnostics indicate that the SMEJ may not be fully controlling the Q2DW’s phase-speed but it is significantly affecting it. Hence, there is a high correlation between them.
Discussion
This study presents a new dynamic by which the SMEJ may be affecting temperature’s Q2DW component. This study reveals that after the Q2DW amplitude reaches peak values, the SMEJ substantially controls its phase-speed by depositing momentum into the wave. Consequently, the SMEJ substantially controls the zonal movements of the decaying Q2DW temperature perturbations. The connection also allows the interannual variabilities of the decay-phase SMEJ wind values to be partially reflected on the decaying-Q2DW phase-speed. Future studies though should investigate the phase-speed of the Q2DW component of other dynamical variables and chemical species. Likewise, future studies should also investigate the phase-speed of other planetary-scale waves. They may exhibit something different but also noteworthy.
This study also suggests that interannual phenomena like ENSO, QBO and the 11-year solar cycle may affect the decaying Q2DW phase-speed via the SMEJ. Previous studies have shown potential connections between these phenomena and the Q2DW but only through the Q2DW amplitudes24,25,26. Likewise, previous studies have also shown potential connections between these and the SMEJ27,28,29,30,31. More observations and model experiments are still needed to fully establish that these interannual phenomena do affect Q2DW phase-speed via the SMEJ. It is still possible that other phenomena may be driving these interannual variabilities.
The results of this study have important implications for whole atmosphere modeling and consequently, space weather forecasting. Space weather forecasting has now become reliant on whole atmosphere models. eCMAM is one of the few models that can self-consistently simulate the Q2DW satisfactorily23. Most whole atmosphere models require data assimilation to simulate the Q2DW16,32,33. However, none of these models can fully simulate the observed dynamics of the Q2DW. Our work adds another Q2DW dynamic that needs to be self-consistently simulated. Consequently, this also adds another challenge to space weather forecasting.
Data and methods
Python 3.11.3 was used for all calculations and generation of figures.
Extended Canadian middle atmosphere model
This work primarily uses 6-hourly model output from eCMAM33,34,35,36,37. eCMAM has a horizontal resolution with a T32 spectral truncation and has 95 vertical levels from the surface extending up to 2 × 10−7 hPa (corresponding to a geopotential height of ~ 250 km depending on solar cycle). It is nudged to the interim version of the European Center for Medium-Range Weather Forecast Reanalysis up to 1 hPa. Pendlebury23 has shown that the use of the Hines gravity wave parameterization plays a major role in the model’s ability to self-consistently simulate Q2DW events. The model outputs range from 1979 till 2010. However, as Pendlebury23 pointed out, these do not necessarily mean each year is a complete representation of the real atmosphere. Nevertheless, we take advantage of the 31 years of model output and the model’s ability to simulate Q2DW events partially constrained by observations through the nudging with ERA-Interim.
Microwave limb sounder onboard the NASA aura satellite
This work uses Aura MLS version 4.2x (V4.2x) temperature vertical profile observations from 2004 to 202339. The MLS temperature profiles have a vertical resolution of 4–6 km in the stratosphere and lower mesosphere as well as 8–13 km in the upper mesosphere. With this vertical resolution, MLS temperature vertical profiles have 55 data points from the stratosphere to the upper mesosphere. The ascending nodes of the Aura orbit, when the spacecraft is moving toward the north, cross the Equator at 13:45 ± 15 LT (short-handed to 14:00 LT hereafter). Similarly, the descending nodes, when the spacecraft is moving toward the south, cross the equator at 01:45 ± 15 LT (short-handed to 02:00 LT hereafter). This orbit allows MLS to supply near-global daily maps of 02:00 LT and 14:00 LT temperature from the stratosphere to the upper mesosphere. This sampling is sufficient to observe the quasi-2-day wave20,21.
Estimating Q2DW Phase-speed
The phase-speed of any wave can be calculated given its period \(P\) (in days) and its latitudinal coordinate \(\phi\) using the formula \(c=-\frac{d}{86400P}\) where \(d=\frac{2}{3}\pi {R}_{E}\mathit{cos}(\phi \pi /180)\). This work focuses on the westward wavenumber 3 quasi-2-day wave. For each latitude-altitude grid point, 2D least-squares fit is employed on a time-series of longitude profiles with a window of 9 days to search between periods \(P\) of 1 to 5 days in increments of 0.05 days for the westward wavenumber-3 wave with the largest amplitude. The basis function for the fit is:
Repeating this process over the same latitude-altitude grid point for multiple days can yield a time-series of amplitude profiles. This gives the amplitude of westward wavenumber-3 waves as a function of period and day-of-year. Converting the period bins into phase-speed bins using equation-1 yields a spectrum like (Fig. 1d). A 9-day window stepped daily is employed in the calculation of Q2DW phase-speed from eCMAM simulations. 9-day window stepped 4 days is employed in the calculation of Q2DW phase-speed from eCMAM simulations due to sampling constraints. Cubic-spline Interpolation was then used to fill out the gaps.
Peak-tracking algorithm for each Q2DW event
To characterize each year’s Q2DW event, we determine its peak Q2DW amplitude as well as the latitude-altitude location of this amplitude as a function of day-of-year from January 1 of each year. Figure S1a–c illustrates our Q2DW peak-tracking algorithm. In this algorithm, we don’t simply aim to find the latitude-altitude gird point of the highest amplitude because this assumes that the Q2DW peaks only over this extremely small point. We first take a zonal profile of Q2DW amplitude. We then convert the entire array south of the equator into a one-dimensional float array. From this array of numbers, we get the 95% percentile value. The histogram in figure S1b illustrates this. Finally, we remove all values less than the 95% percentile value and average the remaining values. The contour plot on the right-side of figure S1c shows the Q2DW amplitude zonal-profile but with areas whose values are greater than the 95% percentile value contour-filled. At the same time, we note the array indices for the remaining values. We take these indices for an array containing the latitude of each grid point as well as an array containing the altitude of each grid point and we average the latitude and altitude values coinciding with these indices. Figure S1d,e show the resulting time-series of this algorithm for model year 2002. They show that this eCMAM Q2DW event in model year 2002 attains peak amplitudes of around 12 K around day-of-year 30. They also show that the peak’s latitude-altitude location hovers between latitude 50S to latitude 20S as well as between altitude 60 and 80 km. It also shows that the location moves poleward and upward as the event progresses.
Multiple linear regression and reconstruction
Multiple linear regression analysis is performed to explore the role of the El nino southern oscillation, the quasi-biennial oscillation, and the 11-year solar cycle on the interannual variability of decaying Q2DW phase-speed. The regression fits the time-series of decaying Q2DW phase-speed and decay-phase SMEJ wind values to the following equation:
In this equation, \(\overline{c }\) is the mean component, \(MEI({t}_{month})\) is the ENSO index called the Multivariate ENSO index, \(QBO({t}_{month})\) is the 30 mb QBO index and \(SC({t}_{month})\) is the solar cycle index called the F10.7 index. All these indices have monthly resolution. To perform the fit, we picked out the indices for January of every year because the decaying Q2DW phase-speed and decay-phase SMEJ wind values are all in roughly the month of January. After fitting, we then reconstruct the time-series using the calculated coefficients \({c}_{1}\), \({c}_{2}\) and \({c}_{3}\) and calculate the correlation between the original time-series and reconstruction to determine how well the reconstruction performs.
Planetary wave diagnostics
The diagnostics that this work uses are the EP Flux, EP Flux divergence, meridional gradient of the quasi-geostrophic Potential Vorticity, and the critical layer7. The EP Flux vectors, and divergence are expressed as:
Here, \({F}^{(\phi )}\) and \({F}^{(z)}\) are the meridional and vertical component of the EP Flux. \({\rho }_{0}\) is atmospheric neutral density. \(u\) is zonal wind. \(v\) is meridional wind. \(w\) is vertical wind. \(\theta\) is potential temperature. \(z\) is geopotential height. \(f\) is the Coriolis parameter. Over-barred terms are daily-mean and zonal-mean components. Primed terms are the Q2DW component of the parameter. Parameters that are sub-scripted denote partial derivatives with respect to this parameter. The meridional gradient of the quasi-geostrophic Potential Vorticity and the refractive index are expressed as:
Here, \(\Omega\) is the angular velocity of the Earth. \({N}^{2}\) is the static stability parameter. \(H\) is the scale-height. The critical layer is determined by calculating \(\overline{u }-c\) and finding lines where \(\overline{u }-c=0\).
This work calculates the 31-year average of these diagnostics on all days after peak-Q2DW-day until the 30th day although we only show the values on the 10, 20 and 30th day. To do this, we first used the same feature-tracking algorithm each model year to determine the exact date that the Q2DW amplitude is highest. We then calculated the planetary wave diagnostics on all days after this day of peak Q2DW amplitude. This gives us 31 years of zonal profile for each planetary wave diagnostics on all days after the peak until the 30th day. Finally, we averaged all 31 years of these profiles.
The 30-year average of these diagnostics on the 10, 20 and 30th day after peak-Q2DW-day is shown in Fig. 6. The left, middle and right columns show the 30-year average of these diagnostics on the 10, 20, and 30th day after peak-Q2DW-day. The top row (Fig. 6a–c) shows the Q2DW amplitude, the EP Flux vectors and areas of positive or negative EP Flux divergence. EP Flux vectors indicate the direction of Q2DW propagation. EP Flux divergence characterizes the momentum transfer between the SMEJ and the Q2DW. For the Q2DW wave, positive values indicate the SMEJ deposits its momentum on the wave while negative values indicate the opposite. Contour-filled regions of the Q2DW amplitude are areas of positive EP Flux divergence while un-filled regions are areas of negative EP Flux divergence. The middle row (Fig. 6d–f) replaces the Q2DW amplitudes in the top row with the EP Flux divergence values. The bottom row (Fig. 6g–i) shows the background zonal wind, the areas where \({\overline{q} }_{\phi }<0\), the critical line \(\overline{u }-c=0\) and the EP Flux vectors. Contour-filled regions of the background zonal wind are areas where \({\overline{q} }_{\phi }<0\) which is a crucial but insufficient condition for baroclinic/barotropic instability.
Data availability
All eCMAM outputs are publicly available to download at https://climate-modelling.canada.ca/climatemodeldata/cmam/cmam30/. MLS data are publicly available to download at https://aura.gsfc.nasa.gov/mls.html. QBO index is accessible from http://www.cpc.ncep.noaa.gov/data/indices/qbo.u30.index. ENSO/MEI index is accessible from https://psl.noaa.gov/enso/mei/. F10.7 index is available at https://omniweb.gsfc.nasa.gov/.
Code availability
The underlying code for this study is not publicly available but may be made available to qualified researchers on reasonable request from corresponding author.
References
Waugh, D. W., Sobel, A. H. & Polvani, L. M. What is the polar vortex and how does it influence weather?. Bull. Am. Meteor. Soc. 98(1), 37–44 (2017).
Overland, J. et al. The polar vortex and extreme weather: The beast from the East in winter 2018. Atmosphere 11(6), 664 (2020).
Pedatella, N. M., Richter, J. H., Edwards, J. & Glanville, A. A. Predictability of the mesosphere and lower thermosphere during major sudden stratospheric warmings. Geophys. Res. Lett. 48(15), e2021GL093716 (2021).
Pedatella, N. M. Influence of stratosphere polar vortex variability on the mesosphere, thermosphere, and ionosphere. J. Geophys. Res. Space Phys. 128(7), e2023JA031495 (2023).
Goncharenko, L. P., Harvey, V. L., Liu, H. & Pedatella, N. M. Sudden Stratospheric Warming Impacts on the Ionosphere–Thermosphere System. In Ionosphere Dynamics and Applications (eds Huang, C., Lu, G., Zhang, Y. & Paxton, L. J.). https://doi.org/10.1002/9781119815617.ch16 (2021).
Woollings, T. et al. The role of rossby waves in polar weather and climate. Weather Clim. Dyn. 4(1), 61–80 (2023).
Yue, J., Lieberman, R. & Chang, L. C. Planetary Waves and Their Impact on the Mesosphere, Thermosphere, and Ionosphere. In Upper Atmosphere Dynamics and Energetics (eds Wang, W., Zhang, Y. & Paxton, L.J.). https://doi.org/10.1002/9781119815631.ch10 (2021).
Knipp, D. J., McQuade, M. K. & Kirkpatrick, D. Understanding Space Weather and the Physics Behind It (McGraw-Hill Education, 2011).
Salby, M. L. The 2-day wave in the middle atmosphere: Observations and theory. J. Geophys. Res. Oceans 86(C10), 9654–9660 (1981).
Plumb, R. A. Baroclinic instability of the summer mesosphere: A mechanism for the quasi-two-day wave?. J. Atmos. Sci. 40(1), 262–270 (1983).
Pfister, L. Baroclinic instability of easterly jets with applications to the summer mesosphere. J. Atmos. Sci. 42(4), 313–330 (1985).
Salby, M. L. & Callaghan, P. F. Seasonal amplification of the 2-day wave: Relationship between normal mode and instability. J. Atmos. Sci. 58(14), 1858–1869 (2001).
Yue, J., Wang, W., Richmond, A. D., & Liu, H. L. Quasi‐two‐day wave coupling of the mesosphere and lower thermosphere‐ionosphere in the TIME‐GCM: Two‐day oscillations in the ionosphere. J. Geophys. Res. Space Phys. 117(A7) (2012).
Yue, J. & Wang, W. Changes of thermospheric composition and ionospheric density caused by quasi 2 day wave dissipation. J. Geophys. Res. Space Phys. 119(3), 2069–2078 (2014).
Wu, D. L., Fishbein, E. F., Read, W. G. & Waters, J. W. Excitation and evolution of the quasi-2-day wave observed in UARS/MLS temperature measurements. J. Atmos. Sci. 53(5), 728–738 (1996).
McCormack, J. P., Coy, L., & Hoppel, K. W. Evolution of the quasi 2‐day wave during January 2006. J. Geophys. Res. Atmos. 114(D20) (2009).
Yue, J., Liu, H. L., & Chang, L. C. Numerical investigation of the quasi 2 day wave in the mesosphere and lower thermosphere. J. Geophys. Res. Atmos. 117(D5) (2012).
Gu, S. Y., Liu, H. L., Dou, X. & Li, T. Influence of the sudden stratospheric warming on quasi-2-day waves. Atmos. Chem. Phys. 16(8), 4885–4896 (2016).
Pancheva, D., Mukhtarov, P., Siskind, D. E. & Smith, A. K. Global distribution and variability of quasi 2 day waves based on the NOGAPS-ALPHA reanalysis model. J. Geophys. Res. Space Phys. 121(11), 11–422 (2016).
Pancheva, D., Mukhtarov, P. & Siskind, D. E. Climatology of the quasi-2-day waves observed in the MLS/Aura measurements (2005–2014). J. Atmos. Solar Terrestrial Phys. 171, 210–224 (2018).
Iimura, H. et al. Climatology of quasi-2-day wave structure and variability at middle latitudes in the northern and southern hemispheres. J. Atmos. Solar Terrestrial Phys. 221, 105690 (2021).
Andrews, D. G., Holton, J. R. & Leovy, C. B. Middle Atmosphere Dynamics (No. 40) (Academic press, 1987).
Pendlebury, D. A simulation of the quasi-two-day wave and its effect on variability of summertime mesopause temperatures. J. Atmos. Solar Terrestrial Phys. 80, 138–151 (2012).
Huang, Y. Y. et al. Global climatological variability of quasi-two-day waves revealed by TIMED/SABER observations. In Annales Geophysicae (eds Huang, Y. Y. et al.) (Copernicus Publications, 2013).
Liu, G., England, S. L. & Janches, D. Quasi two-, three-, and six-day planetary-scale wave oscillations in the upper atmosphere observed by TIMED/SABER over~ 17 years during 2002–2018. J. Geophys. Res. Space Phys. 124(11), 9462–9474 (2019).
Tang, L., Gu, S. Y., Zhao, S. Y. & Wang, D. On the quasi-2-day planetary waves in the middle atmosphere during different QBO phases. Atmos. Chem. Phys. Discuss. 2022, 1–37 (2022).
Baldwin, M. P. et al. The quasi-biennial oscillation. Rev. Geophys. 39(2), 179–229 (2001).
García‐Herrera, R., Calvo, N., Garcia, R. R., & Giorgetta, M. A. Propagation of ENSO temperature signals into the middle atmosphere: A comparison of two general circulation models and ERA‐40 reanalysis data. J. Geophys. Res. Atmos. 111(D6) (2006).
Li, T. et al. Southern hemisphere summer mesopause responses to El Niño-Southern Oscillation. J. Clim. 29(17), 6319–6328 (2016).
Cullens, C. Y., England, S. L. & Garcia, R. R. The 11 year solar cycle signature on wave-driven dynamics in WACCM. J. Geophys. Res. Space Phys. 121(4), 3484–3496 (2016).
Gan, Q. et al. Temperature responses to the 11 year solar cycle in the mesosphere from the 31 year (1979–2010) extended Canadian middle atmosphere model simulations and a comparison with the 14 year (2002–2015) TIMED/SABER observations. J. Geophys. Res. Space Phys. 122(4), 4801–4818 (2017).
Wang, J. C., Chang, L. C., Yue, J., Wang, W. & Siskind, D. E. The quasi 2 day wave response in TIME-GCM nudged with NOGAPS-ALPHA. J. Geophys. Res. Space Phys. 122(5), 5709–5732 (2017).
Sassi, F., McCormack, J. P., Tate, J. L., Kuhl, D. D. & Baker, N. L. Assessing the impact of middle atmosphere observations on day-to-day variability in lower thermospheric winds using WACCM-X. J. Atmos. Solar Terrestrial Phys. 212, 105486 (2021).
Beagley, S. R., McLandress, C., Fomichev, V. I. & Ward, W. E. The extended Canadian middle atmosphere model. Geophys. Res. Lett. 27(16), 2529–2532 (2000).
De Grandpré, J. et al. Ozone climatology using interactive chemistry: Results from the Canadian middle atmosphere model. J. Geophys. Res. Atmos. 105(D21), 26475–26491 (2000).
Fomichev, V. I. et al. Extended Canadian middle atmosphere model: Zonal-mean climatology and physical parameterizations. J. Geophys. Res. Atmos. 107(D10), ACL-9 (2002).
Scinocca, J. F., McFarlane, N. A., Lazare, M., Li, J. & Plummer, D. The CCCma third generation AGCM and its extension into the middle atmosphere. Atmos. Chem. Phys. 8(23), 7055–7074 (2008).
McLandress, C., Plummer, D. A. & Shepherd, T. G. Technical note: A simple procedure for correcting temporal discontinuities in ERA-Interim stratospheric temperatures for use in nudged chemistry-climate model simulations. Atmos. Chem. Phys. 13(25), 801–825 (2013).
Waters, J. W. et al. The earth observing system microwave limb sounder (EOS MLS) on the aura satellite. IEEE Trans. Geosci. Remote Sens. 44(5), 1075–1092 (2006).
Acknowledgements
The work is supported by NASA's Sun-Climate research project at GSFC (WBS 509496.02.03.01.17.04), by Living With a Star (LWS) program (WBS 936723.02.01.12.48) and by GESTAR-2 cooperative agreement with NASA Goddard Space Flight Center. CCJHS is thankful to Prof. Loren C. Chang of the National Central University in Taiwan for helpful discussions.
Funding
Goddard Space Flight Center, WBS 509496.02.03.01.17.04, NASA Living With A Star, WBS 936723.02.01.12.48.
Author information
Authors and Affiliations
Contributions
CCJHS performed calculations and analysis involving the eCMAM model outputs and MLS data. DW performed calculations using the MLS data. DW supervised the analysis. CCJHS wrote the full draft of the manuscript as well as made all the figures. DW helped revise the drafts. DW provided funding. DW came up with the idea for the study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Salinas, C.C.J.H., Wu, D.L. Movement of decaying quasi-2-day wave in the austral summer-time mesosphere. Sci Rep 14, 17387 (2024). https://doi.org/10.1038/s41598-024-68559-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-68559-5