By Manil Suri, Professor of Mathematics and Statistics, UMBC, and Karen Saxe, Macalester College
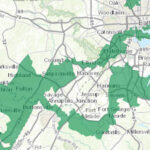
“Are we in Maryland’s third congressional district?” Karen asked on a recent visit to the UMBC campus. Despite zooming into the district’s map on Wikipedia, neither of us could tell. With good reason – “the praying mantis,” as the third has been called, has one of the most flagrantly gerrymandered boundaries in the country. (The university sits just outside, as we later found.)
Welcome to Democrat-controlled Maryland. The state, along with Republican-controlled North Carolina, defended its congressional districting against the charge of unlawful partisan gerrymandering in hearings at the U.S. Supreme Court on March 26.
One might think that a map that confounds two mathematicians must be in clear violation of the law. Indeed, political scientists and mathematicians have worked together to propose several geometrical criteria for drawing voting districts of logical contiguous shapes, which are now in use in various U.S. states.
But here’s the rub: Gerrymandering in itself is not unconstitutional. For the Supreme Court to rule against a particular map, plaintiffs need to establish that the map infringes on some constitutional right, such as their right to equal protection or free expression. This creates a problem. Geometrical criteria don’t detect partisanship. Other traditional criteria, like ensuring each district has the same population, can also be easily satisfied in an otherwise unfairly designed state map.
How then to define a standard to identify partisan gerrymandering that is egregious enough to be illegal? Mathematical scientists have already come up with promising solutions, but we are concerned that the Supreme Court may not take their advice when it issues its decision in June.
Searching for answers
The Supreme Court has grappled with the question of manageable standards at least since 1986 – long enough for Justice Antonin Scalia to declare in a 2004 ruling that since one hadn’t emerged yet, the issue of partisan gerrymandering was not legally decidable, and therefore, no further appeals should be considered.
It was only Justice Anthony Kennedy’s separate concurrence that kept the door open. He cautioned against abandoning the search for a standard too soon, saying that “technology is both a threat and a promise.” In other words, technological advances would probably exacerbate the gerrymandering problem, but they could also provide a solution.
The problem has worsened, just as Kennedy predicted. Computer programs can now generate a profusion of redistricted maps, all of which satisfy traditional constraints such as contiguity and equal population across districts. Then, the majority party can just pick the map most favorable to it.
This was demonstrated in Wisconsin’s 2018 elections. Computer-boosted gerrymandered maps supersized the Republicans’ 13-seat edge to a 25-seat majority, even though Democrats won 53 percent of the total statewide vote.
We expect new congressional districts drawn countrywide after the 2020 census will be subject to even more ferocious computer-driven gerrymandering.
Math to the rescue
But the second part of Kennedy’s prediction has also come true. The same tools that produce drastically gerrymandered maps can be used to draw fair maps.
The first step is to generate – without partisan intent – a vast number of maps that adhere to traditional redistricting criteria. This creates a database against which any proposed map can be compared, by using a suitable mathematical formula that measures partisanship. Through this process, maps with extreme bias will appear as clear outliers, much like data points near the outer ends of a bell curve.
The “efficiency gap” is one such mathematical formula. It measures how efficiently one party’s votes get used and how much the other party’s votes get wasted. For example, a map might pack voters together to minimize their influence in other districts, or spread them out so they don’t form an effective bloc.
Alternative formulas exist as well. In fact, we recommend using a collection of formulas, rather than just one, to compensate for the limitations of each.
Recent conferences on redistricting have seen the mathematics and statistics communities coalesce around this “outlier approach.”
Overcoming skepticism
Getting the Supreme Court to accept this approach, however, will require overcoming the skepticism some conservative justices have expressed toward the use of mathematics and statistics in setting legal standards.
During October 2017 oral arguments for a challenge to the Wisconsin maps, for instance, Chief Justice John Roberts characterized the efficiency gap as “sociological gobbledygook,” while Justice Neil Gorsuch said that the idea of using multiple formulas for measuring gerrymandering was like adding “a pinch of this, a pinch of that” to his steak rub. Roberts also fretted that the country would dismiss statistical formulas as “a bunch of baloney” and suspect the court of political favoritism in adopting them.
At the March 26 hearings for the North Carolina challenge, conservative justices were more measured and mathematically savvy in expressing their reservations. This time, the “outlier approach” took center stage. Affirmed in the lower court decision and explained in an amicus brief, it was also endorsed in oral arguments by Justices Elena Kagan and Sonia Sotomayor. The key doubts came from Justices Samuel Alito, Gorsuch and Brett Kavanaugh, who questioned the feasibility of defining an “outlier” in practice – in particular, setting a range of numerical parameters that would demarcate permissible maps from nonpermissible ones.
The answer to such objections, adeptly addressed in an amicus brief by MIT’s Eric Lander, is twofold. First, the maps being challenged are so biased that they are extreme outliers. They would show up as anomalies under any test for partisanship. So there is no need for the Supreme Court to set a numerical cutoff level at this stage – though a threshold may, indeed, evolve in the future. Secondly, such an extreme outlier approach is already an indispensable tool in several areas of national importance. For example, it is used to test nuclear safety, predict hurricanes and assess the health of financial institutions.
Moreover, this approach has already been shown to work smoothly in gerrymandering cases as well, such as in one from Pennsylvania. Moon Duchin, a Tufts University math professor, used it to analyze – in a report requested by Governor Tom Wolf – newly proposed maps for fairness. A map drawn by the GOP state legislature clearly stood out as an extreme outlier among over a billion maps generated, both when evaluated using the efficiency gap and under another measure of partisanship called the mean-median score. Based on Duchin’s report, the governor rejected the map proposed by the GOP.
We expect that, pushed by citizen groups, an increasing number of states will incorporate math into redistricting procedures. Last year, for instance, Missouri approved Amendment 1, prescribing detailed mathematical rules that must be followed to ensure the fairness of redrawn districts. Although the rules rely heavily on just the efficiency gap – and lawmakers may try to altogether annul them – the fact that ordinary citizens voted overwhelmingly (62 percent to 38 percent) in favor of such a math-incorporating measure is truly precedent-setting.
Such developments were noted in the March 26 oral arguments, when some justices wondered whether, in light of state initiatives, the Supreme Court really had to step in. As the citizens’ attorneys pointed out, however, there are very few states east of the Mississippi where such citizen initiatives are allowed. (North Carolina is not one of them.) It behooves the court to take the lead nationally.
Enhanced by computer power, partisan gerrymandering poses a burgeoning threat to the American way of democracy. Workable standards based on sound mathematical principles may be the only tools to counter this threat. We urge the Supreme Court to be receptive to such standards, thereby enabling citizens to protect their right to fair representation.
* * * * *
Manil Suri, Professor of Mathematics and Statistics, University of Maryland, Baltimore County and Karen Saxe, Professor of Mathematics, Emerita, Macalester College
Header image: Maryland’s third congressional district. Wikimedia
This article is republished from The Conversation under a Creative Commons license. Read the original article.





